Determinan
Determinan adalah nilai yang dapat dihitung dari unsur-unsur suatu matriks persegi. Matriks persegi adalah matriks yang memiliki jumlah baris dan kolom yang sama, sehingga kalau kita gambarkan bentuk matriksnya, akan membentuk bangun layaknya persegi. Misalnya, terdapat suatu matriks yang kita beri nama matriks A. Determinan matriks A bisa ditulis dengan tanda det (A), det A, atau |A|. Nah, cara mencari determinan suatu matriks juga berbeda-beda, tergantung dari ordonya.
Determinan Matriks Ordo 2x2
Misalkan
Adalah matriks berordo 2x2. Elemen a dan d terletak pada diagonal utama, sedangkan elemen b dan c terletak pada diagonal kedua. Determinan matriks A dapat diperoleh dengan mengurangkan hasil kali elemen-elemen diagonal utama dengan hasil kali elemen-elemen diagonal kedua.
Contoh soal
Tentukanlah determinan matriks berikut!
Pembahasan:
Determinan Matriks Ordo 3x3
Misalkan
Adalah matriks berordo 3x3. Terdapat dua cara yang bisa dilakukan untuk mencari determinannya, yaitu menggunakan aturan Sarrus dan metode minor-kofaktor.
Contoh soal
Tentukan determinan matriks berikut ini menggunakan aturan Sarrus dan metode minor-kofaktor!
Pembahasan:
Aturan Sarrus
Agar lebih mudah, kita tulis kembali elemen-elemen pada kolom ke-1 dan ke-2 di sebelah kanan matriks A sebagai berikut:
Hasil kali elemen yang terkena garis putus-putus berwarna biru diberi tanda positif (+), sedangkan hasil kali elemen yang terkena garis putus-putus berwarna oranye diberi tanda negatif (-). Urutan penulisan nya menjadi :
Metode Minor-Kofaktor
Berdasarkan rumus minor-kofaktor di atas, determinan matriks A dapat dicari dengan menghitung jumlah seluruh hasil kali antara kofaktor matriks bagian dari matriks A dengan elemen-elemen pada salah satu baris atau kolom matriks A. Jadi, pertama, kita pilih salah satu baris atau kolom matriks A untuk mendapatkan nilai determinannya. Misalnya, kita pilih baris ke-1. Elemen-elemen matriks baris ke-1, yaitu a11, a12, dan a13.
Selanjutnya, karena kita pilih elemen-elemen pada baris ke-1, rumus determinan matriks yang kita gunakan adalah sebagai berikut:
Langkah kedua, kita cari kofaktor matriks bagian dari matriks A (Cij). Cij = (-1)i+j Mij dan Mij = det Aij dengan Aij merupakan matriks bagian dari matriks A yang diperoleh dengan menghilangkan baris ke-i dan kolom ke-j.
Sebelumnya, kita telah memilih elemen-elemen pada baris ke-1, yaitu a11, a12, dan a13. Oleh karena itu, matriks bagian dari matriks A nya adalah A11, A12, dan A13.
•A11 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-1.
•A12 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-2.
•A13 diperoleh dengan menghilangkan elemen-elemen pada baris ke-1 dan kolom ke-3.
Sehingga
Invers matriks
Invers matriks adalah kebalikan (invers) dari sebuah matriks. Jadi, apabila matriks tersebut dikalikan dengan inversnya, maka akan menjadi matriks identitas. Pada fungsi invers, kita disuruh mencari kebalikan dari fungsi tersebut. Misalnya, invers dari f(x) = 2x, maka jawabannya adalah f-1 (x) = ½ x.
Invers Matriks Ordo 2x2
Tentukan invers Matriks berikut
Pembahasan:
Invers Matriks Ordo 3x3
Mencari invers matriks berordo 3x3 dapat dilakukan dengan dua cara, yaitu dengan adjoin dan transformasi baris elementer.
Contoh soal:
Penyelesaian:
Daftar pustaka
Mencari Determinan dan Invers Matriks | Matematika Kelas 11. Ruang guru. 2022.

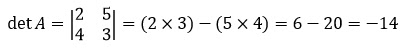










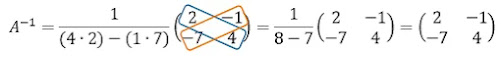




Komentar
Posting Komentar