LIMIT
A. LIMIT FUNGSI ALJABAR
Limit dapat diartikan sebagai menuju suatu batas, sesuatu yang dekat namun tidak dapat dicapai. Dalam bahasa matematika, keadaan ini dapat disebut limit. Mengapa harus ada limit? limit menjelaskan suatu fungsi jika batas tertentu didekati. Mengapa harus didekati? karena suatu fungsi biasanya tidak terdefinisi pada titik-titik tertentu. Walaupun suatu fungsi seringkali tidak terdefinisi untuk titik tertentu, namun masih dapat dicari tahu berapa nilai yang didekati oleh fungsi tersebut apabila titik tertentu semakin didekati yaitu dengan limit.
Dalam bahasa matematika, limit dituliskan dengan:
Toerema / Pernyataan:
Suatu fungsi dikatakan mempunyai limit apabila antara limit kiri dan limit kananya mempunyai besar nilai yang sama dan apabila limit kiri dan limit kanan tidak sama maka nilai limitnya tidak ada.
Sifat-sifat Limit Fungsi Aljabar
Apabila n merupakan bilangan bulat positif, k konstanta, f dan g adalah fungsi yang mempunyai limit di c, maka sifat-sifat di bawah ini berlaku.
Menentukan Nilai Limit Fungsi Aljabar
Ada 2 bentuk dalam menentukan limit fungsi aljabar yaitu:
Bentuk pertama
Bentuk kedua
Dalam hubungannya dengan bentuk limit yang pertama ada beberapa metode dalam menentukan nilai limit fungsi aljabar yaitu dengan cara substitusi dan cara pemfaktoran
Cara substitusi ini langkahnya dengan mengganti peubah yang mendekati nilai tertentu dengan fungsi aljabarnya. Berikut adalah beberapa contoh yang dapat dipahami.
Contoh 1:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
Cara Pemfaktoran
Cara pemfaktoran digunakan apabila cara substitusi menghasilkan nilai limit yang tidak terdefinisikan seperti pada contoh berikut:
Cara pemfaktoran dilakukan dengan langkah menentukan faktor persekutuan antara pembilang dan penyebuntya. Berikut beberapa contoh untuk dipahami.
Contoh 1:
Tentukan nilai limit fungsi aljabar dari
Jadi, nilai dari limit fungsi aljabar tersebut,
B. Teorema limit
Limit dalam bahasa umum bermakna batas. Definisi dari limit ini menyatakan bahwa suatu fungsi f(x) akan mendekati nilai tertentu jika x mendekati nilai tertentu. Pendekatan ini terbatas antara dua bilangan positif yang sangat kecil yang disebut sebagai epsilon dan delta. Hubungan ke-2 bilangan positif kecil ini terangkum dalam definisi limit.
Limit 0/0
Bentuk 0/0 kemungkinan timbul dalam
ketika kita menemukan bentuk seperti itu coba untuk sederhanakan fungsi tersebut.
Jika itu bentuk persamaan kuadrat kita bisa coba memfaktorkan atau dengan cara asosiasi, dan jangan lupa aturan a2-b2 = (a+b) (a-b).
Berikut adalah contohnya :
Limit ∞/∞
Bentuk limit ∞/∞ terjadi pada fungsi suku banyak (polinom) seperti
Rumus cepat limit bentuk ∞/∞
- Jika m<n maka L = 0
- Jika m=n maka L = a/p
- Jika m>n maka L = ∞
Limit (∞-∞)
Bentuk (∞-∞) sering sekali muncul pada saat ujian nasional.
Bentuk soalnya sangat beragam. Namun, penyelesaiannya tidak jauh dari penyederhanaan.
Jika disubstitusikan x -> 1 maka bentuknya akan mmenjadi (∞-∞).
Dan untuk menghilangkan bentuk ∞-∞ kita sederhanakan bentuk tersebut menjadi
Rumus Cepat limit tak hingga
Rumus cepat mengerjakan limit tak hingga yang pertama dapat digunakan untuk bentuk soal limit tak hingga pada bentuk pecahan.
Untuk memperoleh nilai limit tak hingga bentuk pecahan kita hanya perlu memperhatikan pangkat tertinggi dari masing-masing pembilang dan penyebut.
Ada 3 kemungkinan yang dapat saja terjadi.
Pertama, pangkat tertinggi pembilang lebih kecil dari pangkat tertinggi penyebut.
Kedua, pangkat tertinggi pembilang sama dengan pangkat tertinggi penyebut.
Ketiga, pangkat tertinggi pembilang lebih tinggi dari pangkat tertinggi penyebut.
Rumus ke-3 nilai limit tak terhingga bentuk pecahan tersebut dapat dilihat pada persamaan dibawah ini.
Nilai pangkat tertinggi pada pembilang adalah 3. Nilai pangkat tertinggi penyebut adalah 2 (m>n). Jadi, nilai limitnya adalah ∞.
C. LIMIT TAK TENTU
Kalian pasti tidak asing lagi dengan bentuk limit di atas. Ketiga bentuk limit tersebut memiliki penampilan yang sama yaitu terdapat hasil bagi dan memiliki pembilang dan penyebut berlimit nol. Khusus untuk limit yang ketiga sebenarnya merupakan definisi turunan
menghitung limit itu dengan mensubstitusikan nilai x.
pada fungsi pembilang dan penyebut, kita akan memperoleh jawaban yang tak ada artinya, yaitu 0/0. Namun demikian, kita tidak mengatakan bahwa limit tersebut tidak ada, melainkan kita hanya mengatakan bahwa limit tersebut tidak dapat ditentukan dengan aturan hasil bagi limit.
Anda tentunya masih ingat bahwa dengan menggunakan geometri, kita dapat membuktikan bahwa
Di lain pihak, dengan menggunakan pemfaktoran dalam aljabar, kita peroleh
Kita telah berhasil menyelesaikan dua bentuk limit di atas dengan menggunakan geometri dan pemfaktoran aljabar, tetapi tentunya akan lebih baik bila ada aturan baku yang dapat dipakai untuk menghitung limit-limit demikian. Memang ada, yaitu suatu aturan yang lazim dinamakan Aturan I’Hopital (baca: loupital).
Aturan I’Hopital.
Pada tahun 1696, Guillaume Francois Antoine de I’Hopital menerbitkan buku pertama tentang kalkulus diferensial; di dalamnya ada aturan di bawah ini, yang ia peroleh dari gurunya bernama Johann Bernoulli.
TEOREMA: Aturan I'Hopital
ada, baik ia terhingga atau tak-terhingga (misalnya, bilangan terhingga L, ∞,atau-∞), maka
Mari kita lihat beberapa contoh penerapan dari aturan I’Hopital.
CONTOH 1:
Gunakan aturan I’Hopital untuk membuktikan bahwa
Jika kita mensubstitusikan nilai x pada fungsi pembilang dan penyebut, kita akan peroleh dua limit tersebut berbentuk 0/0. Oleh karena itu, kita dapat menggunakan aturan I’Hopital yaitu sebagai berikut.
Jadi, limit yang pertama adalah 1 dan limit yang kedua adalah bernilai 0.
Daftar pustaka
Bunyan. Jagostat. 2021
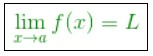

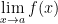

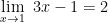




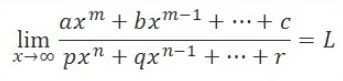












Komentar
Posting Komentar