TURUNAN FUNGSI ALJABAR

 A. Turunan fungsi aljabar dan rumus rumus turunan

Turunan fungsi atau juga bisa disebut dengan diferensial adalah fungsi lain dari suatu fungsi sebelumnya, contohnya fungsi f dijadikan f' yang mempunyai nilai tidak memakai aturan dan hasil dari fungsi akan berubah sesuai dengan variabel yang dimasukan, atau secara umum suatu besaran yang berubah seiring perubahan besaran lainnya. Proses dalam menemukan turunan disebut sebagai diferensiasi. Lalu untuk pengertian turunan aljabar adalah perluasan dari materi limit fungsi.

Notasi turunan fungsi aljabar seperti berikut:

Seperti yang telah disebutkan di atas, jika turunan fungsi aljabar merupakan perluasan dari materi limit fungsi sehingga dapat didefinisikan seperti berikut:

Rumus Turunan Aljabar

Setelah memahami tentang pengertian dari turunan fungsi aljabar, hal yang perlu Sobat Pintar pelajari adalah rumus dari turunan fungsi aljabar. Rumus turunan fungsi aljabar ini terbagi menjadi beberapa rumus berikut:

Turunan Fungsi Pangkat

Turunan Hasil Kali Fungsi

Bentuk dari fungsi kali adalah f(x) = u(x) . v(x), sehingga turunannya adalah f’(x) = u’(x)v(x) + u(x)v’(x).

Turunan Fungsi Pembagian

Contoh Soal:

Turunan Pangkat dari Fungsi

Contoh Soal:

B. PERSAMAAN GARIS SINGGUNG KURVA MENGGUNAKAN TURUNAN

Konsep selanjutnya yang perlu dipelajari tentang turunan fungsi aljabar adalah tentang aplikasi turunan fungsi aljabar. Terdapat beberapa contoh turunan fungsi aljabar yang mana dari setiap aplikasinya terdapat konsep masing-masing yang perlu dipahami. Berikut merupakan aplikasi turunan fungsi aljabar:

1. Menentukan gradien garis singgung suatu kurva

Gradien garis singgung (m) pada suatu kurva y = f(x) dirumuskan sebagai: M = y’ = f’(x)

2. Menentukan interval fungsi naik dan fungsi turun

a. Syarat interval fungsi naik : f'(x) > 0

b. Syarat interval fungsi turun : f'(x) < 0

3. Menentukan nilai stasioner suatu fungsi dan jenisnya

Jika fungsi y = f(x) kontinu dan diferensiabel di x = a dan f'(x) = 0, maka fungsi memiliki nilai stasioner di x = a. Jenis nilai stasioner dari fungsi y = f(x) dapat berupa nilai balik minimum, nilai balik maksimum, atau nilai belok. Jenis nilai stasioner ini bisa ditentukan dengan menggunakan turunan kedua dari fungsi tersebut.

4. Menyelesaikan soal limit berbentuk tak tentu

Jika limit merupakan limit berbentuk tak tentu 0/0, maka penyelesaiannya dapat menggunakan turunan, yaitu f(x) dan g(x) pada masing-masing turunan. Jika dengan turunan pertama sudah dihasilkan bentuk tertentu, maka bentuk tertentu itu adalah penyelesaiannya. Tetapi jika dengan turunan pertama masih dihasilkan bentuk tak tentu, maka masing-masing f(x) dan g(x) diturunkan lagi sampai diperoleh hasil berbentuk tertentu.

C.  MASALAH KONTEKSTUAL MENGGUNAKAN TURUNAN 1 DAN 2 SERTA TITIK STASIONER DARI KURVA

Apa Itu Titik Stasioner?

Titik stasioner merupakan sebuah titik dalam grafik yang turunan kurva pertamanya sama dengan nol. Titik ini disimbolkan dengan rumus berikut:

Supaya lebih mudah dipahami, titik stasioner dapat digambarkan dalam garis fungsi seperti gambar di bawah ini.

Garis fungsi yang menunjukkan titik stasioner (Arsip Zenius)

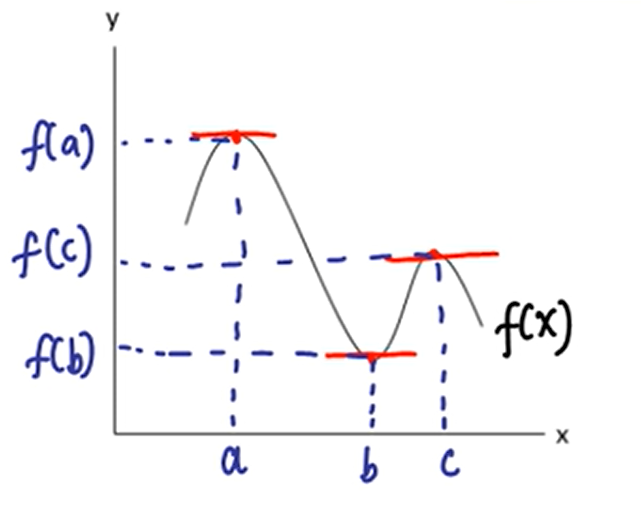
Pada garis fungsi ini, bisa menemukan tiga titik. Pertama, pada saat nilai x=a, sehingga fungsinya disebut sebagai f(a). Kemudian, titik stasioner selanjutnya muncul saat nilai x=b, fungsinya disebut sebagai f(b). Lalu yang terakhir muncul saat nilai x=c, sehingga fungsinya adalah f(c).

Oleh karena itu, titik stasionernya adalah:

• (a, f(a))
• (b, f(b))
• (c, f(c))

juga bisa menyebut bahwa nilai stasionernya adalah:

• f(a)
• f(b)
• f(c)

Cara Menentukan Titik Stasioner

Lalu, bagaimana cara menentukan titik stasioner? Coba ikuti contoh soal berikut.

Tentukan titik stasioner fungsi berikut:

Ingat, nilai fungsi dari titik stasioner harus sama dengan nol (f’(x)=0). Sehingga, turunan dari fungsi ini adalah:

Sehingga, mendapatkan nilai x:

Sekarang, hanya perlu menentukan nilai f(x) untuk mendapatkan titik stasioner dengan memasukkan nilai x. Pertama, harus mencari nilai fungsi f(-3).

Berarti pada fungsi f(-3), titik stasioner ada pada titik (-3,31). 

Selanjutnya, cari nilai fungsi f(1).

Artinya, pada fungsi f(1), titik stasioner ada pada titik (1,-1).

Salah satu nilai stasioner pada grafik berikut ini adalah ….

a. 5

b. 6

c. 4 ½ 

d. 4

e. 1 ½

Nilai stasioner adalah nilai y dari titik stasioner. Dari gambar, dapat dilihat bahwa titik-titik stasionernya adalah (1,6), (4,½), dan (6,3½). Jadi, nilai stasionernya adalah 6, ½, dan 3½. Pada pilihan jawaban yang tersedia, jawaban yang benar adalah b. 6.

Daftar pustaka

Aku pintar. 2022. Zenius. 2022