Regi Diana Savitri

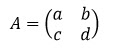
Determinan Determinan adalah nilai yang dapat dihitung dari unsur-unsur suatu matriks persegi. Matriks persegi adalah matriks yang memiliki jumlah baris dan kolom yang sama, sehingga kalau kita gambarkan bentuk matriksnya, akan membentuk bangun layaknya persegi. Misalnya, terdapat suatu matriks yang kita beri nama matriks A. Determinan matriks A bisa ditulis dengan tanda det (A), det A, atau |A|. Nah, cara mencari determinan suatu matriks juga berbeda-beda, tergantung dari ordonya. Determinan Matriks Ordo 2x2 Misalkan Adalah matriks berordo 2x2. Elemen a dan d terletak pada diagonal utama, sedangkan elemen b dan c terletak pada diagonal kedua. Determinan matriks A dapat diperoleh dengan mengurangkan hasil kali elemen-elemen diagonal utama dengan hasil kali elemen-elemen diagonal kedua. Contoh soal Tentukanlah determinan matriks berikut! Pembahasan: Determinan Matriks Ordo 3x3 Misalkan  Adalah matriks berordo 3x3. Terdapat dua cara yang bisa dilakukan untuk mencari determinannya, yaitu

MATRIKS Matriks adalah sekumpulan bilangan yang disusun berdasarkan baris dan kolom, serta ditempatkan di dalam tanda kurung. Nah, tanda kurungnya ini bisa berupa kurung biasa “( )” atau kurung siku “[ ]”. Suatu matriks diberi nama dengan huruf kapital, seperti A, B, C, dan seterusnya.  Jenis-jenis Matriks a. Matriks Baris Matriks baris adalah suatu matriks yang terdiri dari satu baris aja. Contohnya, matriks A, matriks P, dan matriks Q, semuanya terdiri dari satu baris dan beberapa kolom. Untuk masing-masing ordonya, berarti A1x3, P1x4, dan Q1x5 b. Matriks Kolom Kebalikannya dari matriks baris, matriks kolom adalah suatu matriks yang terdiri dari satu kolom saja. Contohnya, Matriks R, matriks S, dan matriks T sama-sama terdiri dari satu kolom dan beberapa baris. Oleh karena itu, ordo matriksnya adalah R2x1, S3x1, dan T4x1. C. Matriks Persegi Matriks persegi adalah suatu matriks yang memiliki jumlah baris dan kolom sama. D. Matriks Diagonal Matriks diagonal adalah matriks persegi yang

  PROGRAM LINEAR Materi program linear  Program linear merupakan salah satu metode dalam menentukan solusi optimal dari suatu permasalahan linear. Dalam program linear terdapat fungsi objektif atau fungsi tujuan. Syarat, batas, dan kendala dalam program linear merupakan suatu bentuk pertidaksamaan linear. Program Linear dalam Kehidupan Sehari-hari Program linear banyak diterapkan dalam berbagai bidang. Dalam bidang matematika dan ekonomi, program linear dapat digunakan sebagai salah satu teknik optimasi produksi dalam suatu pabrik maupun suatu perusahaan. Dalam bidang farmasi, program linear juga dimanfaatkan untuk menentukan dan memodelkan pengoptimasian produksi obat. Hampir semua bidang memanfaatkan program linear sebagai metode dalam melakukan optimasi. Dengan menggunakan program linear kegiatan-kegiatan (misalnya produksi di pabrik, produksi obat, dan lain-lain) akan optimal, sehingga perusahaan memiliki keuntungan yang lebih besar jika dibandingkan dengan tidak memanfaatkan progr

INDUKSI MATEMATIKA   Pengertian Induksi Matematika Induksi matematika adalah cara atau teknik pembuktian secara deduktif dalam matematika. Pembuktian yang dimaksud adalah pembuktian pernyataan-pernyataan yang berkaitan dengan bilangan bulat positif (non negative). Langkah-langkah Induksi Matematika Andaikan p(n) adalah sebuah pernyataan dengan variabel bebas n dan n adalah bilangan bulat positif, maka untuk membuktikan bahwa p(n) benar kita perlu melalui 3 langkah sebagai berikut: 1. Tunjukkan bahwa p(1) benar 2. Misalkanlah p(n) benar untuk semua bilangan bulat positif dengan n ≥ 1 3. Tunjukkan bahwa p(n+1) benar Contoh Soal Induksi Matematika 1. Tunjukkan bahwa 1 + 2 + 3 + … + n =  n(n+1)/2  Pembahasan   Akan ditunjukkan bahwa p(1) benar Jika n = 1, maka: 1 = 1(1+1)/2  = 1 (benar) Misal p(n) benar untuk n ≥ 1, maka: 1 + 2 + 3 + … + n = n(n+1)/2  benar Akan dibuktikan bahwa p(n+1) benar, yaitu: 1 + 2 + 3 + … + n + (n+1) = (n+1) (n+2)/2 Bukti: 1 + 2 + 3 + … + n + (n+1) = n(n+1)/2  + (